Why is it important?
A Zero-Knowledge Proof (ZKP) is a protocol that verifies whether certain knowledge exists without revealing it. In a ZKP two parties perform an exchange where one party proves to the other party that they know a secret without giving away any sensitive information about the secret. If an adversary were to sit in the middle and listen to the exchange, they would not learn the secret or any other information that could lead them to infer the secret. This is because the only information verified by a ZKP is that the proving party knows the secret. The verifying party does not learn what the secret is and cannot obtain or reconstruct the secret in any form.
In a world of password-based authentication and digital privacy, this could be a game-changer to modern cybersecurity. Many methods in cybersecurity involve addressing problems like:
- How do I enroll in services without entering sensitive information?
- How do I prove my identity without giving away my social security number?
- How do I protect my password from hackers on the internet?
ZKP has the potential to solve these problems and others by allowing services to verify necessary information without the user ever disclosing it. This removes the concern of third-party services storing sensitive information in a database, and the user does not need to send it over an unsecure network.
How does it work?
Suppose there is a $100,000 prize to anyone who can find an algorithm that solves a specific type of puzzle. Peggy claims that she has found such an algorithm, but she doesn’t want to give it away in case someone else claims the prize money. Let’s assume that so far no one other than Peggy has been able to come up with a solution. How does Victor verify that Peggy has found an algorithm?
Victor can perform a Zero-Knowledge Proof by generating a random variation of the puzzle and sending it to Peggy. Let’s assume that Victor does not know the solution beforehand but can easily verify if Peggy’s solution is correct (e.g. you can verify a Sudoku puzzle by checking that all rows and columns add up to 9). If Peggy truly knows an algorithm, she can fill in the puzzle and return the answer to Victor. Then, he can confirm that her solution is correct. But what if he is unconvinced? What if Peggy guessed the solution? Then, Victor can repeat the exchange and send another randomly generated puzzle and Peggy can provide him with another solution. With each iteration, the likelihood that Peggy guessed the solution multiple times in a row decreases exponentially. Victor can continue to challenge Peggy with puzzles until he is convinced that she must know an algorithm and it is highly improbable for her to have guessed correctly so many times. Note that by filling in the puzzle, Peggy is not giving away her algorithm, and by receiving the solution Victor cannot presume how Peggy came up with her answer. Thus, Peggy’s secret, the algorithm, remains confidential.
This is just a simplified example of how ZKP can be used to verify a condition (e.g. Peggy knows an algorithm), but how can this be used in cybersecurity? Computers today can perform ZKPs by repeating a series of mathematical tests (i.e. “validating the puzzle”). If Victor prompts Peggy with a “puzzle” or any sort of question like “Do you know the password?”, Peggy’s answer is obscured by a mathematical function. What Peggy sends Victor is not her answer, but something that is mathematically derived from her answer, thus hiding the original answer. With each iteration, the probability of Peggy repeatedly guessing the correct answer decreases. Some ZKPs also insert a small amount of randomness into each exchange to ensure that the same answers don’t produce the same results for following iterations.
How is it secure?
The highlight of ZKP compared to other security protocols is that anything sent across the network or stored in a database cannot be used to recreate the secret. It is infeasible to reverse engineer Peggy’s obscured answer to obtain the original answer because the obscured answer was derived using a special class of mathematical one-way functions that cannot be solved with modern computing. Knowing the outputs of these functions is currently not enough to reconstruct the inputs. A fundamental part of ZKP’s security is also tied to the number of “puzzles” or challenges Victor sends. Suppose there were 10 possible answers to each puzzle. Peggy would have a 1/10 chance of guessing the right answer on the first exchange, a 1/100 chance of guessing two right answers in a row, and a 1/1000 chance of guessing three right answers in a row. This pattern continues with every iteration until Victor decides that it is effectively impossible for Peggy to have guessed each correct answer. Notice that with each iteration the probability that Peggy guessed each answer approaches zero but will never reach it [Figure 1]. We must decide on a cutoff point that is close enough to zero that we are confident that Peggy could not be so precise without knowing the secret. As the number of possible answers for each challenge increases, the cutoff point is reached with fewer iterations.
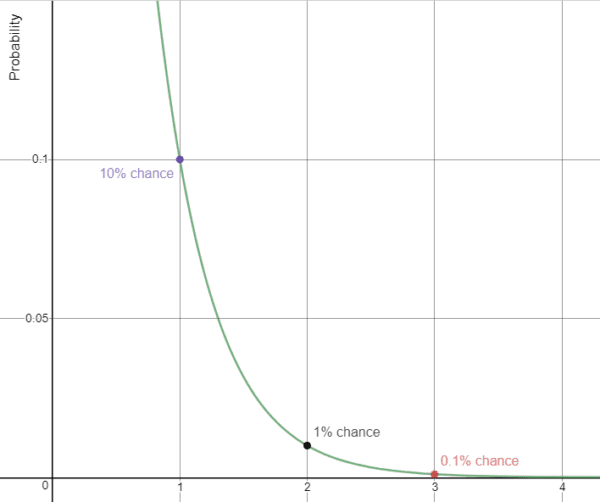
Figure 1: The probability that Peggy will guess the answer for each iteration if there are 10 possible answers.

 Español
Español