When in an online environment, many utilize encryption to protect their communications and personal data. Any encryption method will make data inherently safer than letting it remain unencrypted. How could one make an informed decision as to which cryptographic technique is right for them? We can turn to bits of security – a hypothetical measure of an encryption’s functional strength.

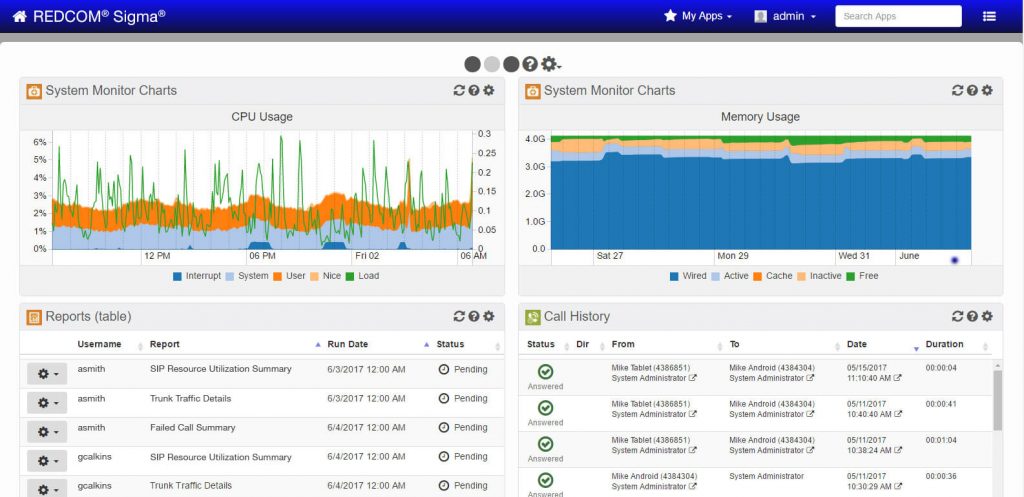
Cryptographic algorithms vary greatly and can be difficult to compare directly. By using bits of security, we can draw a meaningful comparison between cryptographic methods. We use bits of security to analyze the strengths of Advanced Encryption Standard (AES), Rivest-Shamir-Adleman (RSA), and Elliptic Curve Cryptography (ECC).

Bits of security are defined by the number of operations needed to break an encryption algorithm by brute-force attack. If an encryption scheme is rated at 80 bits of security, for example, we can say that a malicious adversary would have to perform 2⁸⁰ operations in order to break that encryption.

AES, a symmetric key algorithm, uses the same key to encrypt and decrypt data. AES keys are generated from random numbers of predetermined size. Popular sizes for AES keys include 128-bits, 192-bits, and 256-bits. For an AES-128 key, any random number from 0 to 2¹²⁸ – 1 can be used, leaving 2¹²⁸ options for key generation. An adversary hoping to derive an AES-128 key by way of brute force has 2¹²⁸ options to try and thus has 2¹²⁸ operations to perform, allowing us to contend that AES-128 offers 128 bits of security.

RSA, an asymmetric algorithm, uses multiplication of large prime numbers to generate a modulus of a certain size. For example, RSA-3072 requires multiplying two prime numbers such that their product is of length 3072 bits. A public and private key pair are generated via this modulus and can be used to send and receive secure messages. When attempting to crack RSA encryption, the main goal is to factor the modulus which was used to create the public & private keys. By analyzing the frequency of prime suitable prime numbers and the latest factoring algorithms, we contend that RSA-3072 offers 128 bits of security.

ECC, another asymmetric encryption algorithm, utilizes elliptic curves over certain number spaces in order to encrypt messages. ECC keys are generated from points on a specific elliptic curve and multiplicative factors that are also derived from this curve. A brute-force cracking attempt on ECC encryption is computing a discrete logarithm in a prime order elliptic group [6]. Several algorithms exist for solving these types of problems. By analyzing ECC against the most effective of these algorithms, we calculate a security level for different ECC keys. To obtain 128 bits of security, an ECC public key would need a length of 256 bits.

Below shows the relative strengths of AES, RSA, and ECC key size needed in bits.